 is an integer such that
is an integer such that
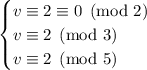
Since 2, 3, and 5 are mutually coprime, you can use the Chinese remainder theorem directly.
Suppose

Then taken mod 2, the last two products vanish and you're left with a remainder of 0 (since 2 divides 2*3*5);
taken mod 3, the first and last products vanish and you're left with a remainder of 2 (since 2*2*5 = 20, and 20 = 2 mod 3);
and taken mod 5, the first two products vanish and you're left with a remainder of 2 (since 2*2*3 = 12, and 12 = 2 mod 5).
So we have
 , and
, and
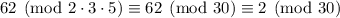 , so that any integer of the form
, so that any integer of the form
 satisfies the system of congruences, the largest of which is 242.
satisfies the system of congruences, the largest of which is 242.