Question

Determine which equation is parallel to the line JK and which is perpendicular to like JK

Answer 1

You havent showed us a picture of the graph so how are we going to help you

Explanation:

Answer 2

If the equation of JK is y = mx + c, then y = mx + c' is the equation of the straight line parallel to above and
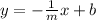`y = - (1)/(m)x + b` will be perpendicular to that.

Explanation:

Let us assume that the line JK has the equation in slope-intercept form as

y = mx + c ............. (1)

Therefore, the equation has slope = m

Now, any straight line having an equation with slope m will be parallel to line JK.

So, the equation of the straight line which is parallel to equation (1) will be

y = mx + c', where, c' is any real constant.

Now, let us assume that another straight line having equation

y = nx + a is perpendicular to the line JK i.e. equation (1).

Now, we know if two lines are perpendicular to each other then the product of their slopes will be - 1.

So, mn = - 1

⇒
`n = - (1)/(m)`

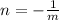
Therefore, the equation of a straight line which is perpendicular to equation (1) will be
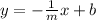`y = - (1)/(m)x + b` where b is any real constant. (Answer)