Question

What average force is necessary to bring a 50.2-kg sled from rest to a speed of 2.8 m/s in a period of 20.1 s?

Answer 1

To solve this problem we will use the concepts related to the Impulse-Momentum Theorem for which it is specified as the product between force and change in time

`\Delta p = F\Delta t`

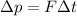
And

\Delta p = m\Delta v

Where,

`F = Force`

`\Delta t = \text{Change in Time}`

`\Delta v = \text{Change in velocity}`

`m = mass`

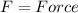
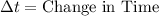
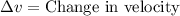
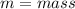
Rearranging to find the Force we have that

`F = (\Delta p)/(\Delta t)`

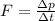
Using the expression between mass and velocity

`F = (m(v_f-v_i))/(\Delta t)`

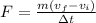
Our values are given as,

`m = 50.2kg\\v_i = 0m/s \\v_f = 2.8m/s \\\Delta t = 20.1s`

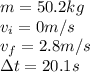
Then replacing we have that

`F = 6.99N`

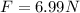
Therefore the average force is 6.99N