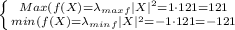Question

Find the absolute maximum and minimum of the function f(x,y)=x^2−y^2f(x,y)=x^2−y^2 subject to the constraint x^2+y^2=121x^2+y^2=121.

Answer 1

The absolute maximum of f(x,y) is 121. The absolute minimum of f(x,y) is -121

Explanation:

The given function f(x,y) can be seen as a quadratic form:

`f(x,y)=(x,y)\left[\begin{array}{cc}1&0\\0&-1\end{array}\right](x,y)^(T)=X^(T)AX`

The constraint can be seen as:

`f(x,y)=(x,y)\left[\begin{array}{cc}1&0\\0&1\end{array}\right](x,y)^(T)=121\\X^(T)IX=X^(T)X=|X|^2=121`

Using the Min-max theorem with Rayleigh–Ritz quotient, we can easly obtain the absolute maximum and minimum of a quadratic form:

`\lambda_(minf)\leq (f(x,y))/(|X|^2) \leq \lambda_(Maxf)`

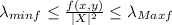
Therefore:

`\left \{ {X \atop X} \right.`

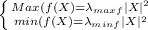
So the problem is reduced to obtain the maximum and minimum eigenvalues of the matrix A.

This eigenvalues ​​can be obtained directly (diagonal matrix), where
`\lambda_(minf)=-1` and
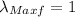`\lambda_(Maxf)=1`. Therefore:

`\left \{ {^2=1 \cdot 121=121 \atop min(f(X)=\lambda_(minf)} \right.`