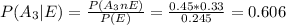Answer:
a)
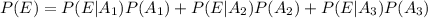
Since we have all the possible values we can replace:
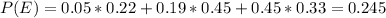
And that would be the proportion of residents who use E-Harmony
We can find the P(A1nE) and P(A2nE) with the following formulas:
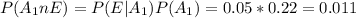
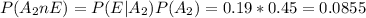
b) For this case we want this probability
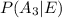
And from the Bayes conditional probability we have this:
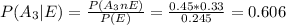
Explanation:
Notation
 represent the event resident between 18 and 29 years old
represent the event resident between 18 and 29 years old
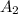 represent the event resident between 30 and 49 years old
represent the event resident between 30 and 49 years old
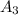 represent the event resident is >50 yeard old
represent the event resident is >50 yeard old
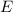 represent the event the residen tuse E-Harmony
represent the event the residen tuse E-Harmony
From the problem we have the following probabilities:
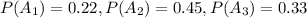
And we have conditional probabilites also given:
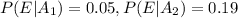
The other probability assumed since the problem is incomplete is:
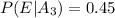
Part a
For this case we can use the total probability rule given by:
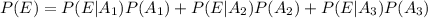
Since we have all the possible values we can replace:
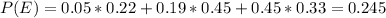
And that would be the proportion of residents who use E-Harmony
We can find the P(A1nE) and P(A2nE) with the following formulas:
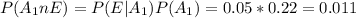
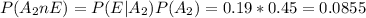
Part b
For this case we want this probability
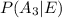
And from the Bayes conditional probability we have this: