The principal sum to be deposited is $ 551.26
Solution:
Given that,
Amount after 10 years = $ 1000
Rate of Interest = 6 % compounded quarterly
Number of years = 10 years
Principal = ?
The formula for compound interest, including principal sum, is:
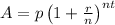
Where,
A = the future value of the investment/loan, including interest
P = the principal investment amount (the initial deposit or loan amount)
r = the annual interest rate (decimal)
n = the number of times that interest is compounded per unit t
t = the time the money is invested or borrowed for
Since interest is compounded quarterly, n = 4

Substituting the values in formula,
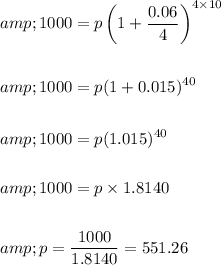
Thus the principal sum to be invested is $ 551.26