Question

Joe is driving west at 60km/h and Dave is driving south at 70 km/h. Both cars are approaching the intersection of the two roads. At what rate is the distance between the cars decreasing when Joe's car is 0.4 km and Dave's is 0.3 km from the intersection

Answer 1

90 km/h

Explanation:

Given: Joe´s speed= 60km/h

Dave´s speed= 70km/h

Now, we need to use vector theory to find the rate at which the distance between the cars decreasing when Joe's car is 0.4 km and Dave's is 0.3 km from the intersection.

∴ Let the intersection be the origin and time (t) will be 0 .

And let the distance between the car be "s"

We know, distance (d)= speed (s)\time (t)

∴ Joe´s distance
`(d_1)= 60* t= 60t`

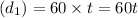
Dave´s distance
`(d_2)= 70* t= 70t`

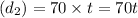
Now, Joe´s change in position is Vector=
`(0.4-60t,0)`

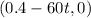
Dave´s change in position is Vector=
`(0, 0.3-70t)`

Next, find the distance between the cars

`s^(2) = (change\ in\ distance\ of\ Joe\ car)^(2)+(change\ in\ distance\ of\ Dave\ car)^(2)`

⇒
`s^(2) = (0.4-60t)^(2)+(0.3-70t)^(2)`

⇒
`s^(2) = (0.4^(2)-2* 0.4* 60t+3600t^(2) )+(0.3^(2) -2* 0.3* 70t+4900t^(2) )`

⇒
`s^(2) = (0.16-48t+3600t^(2) )+(0.09 -42t+4900t^(2) )`

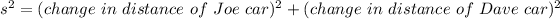
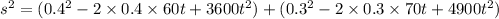
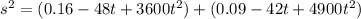
Opening parenthesis

⇒
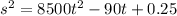`s^(2) = 8500t^(2)-90t+0.25`--- equation (1)

We know, t=0 at the point of intersection of two roads.

∴
`s^(2) = 0.25`

`s=√(0.25) =0.5`

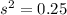
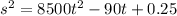`s^(2) = 8500t^(2)-90t+0.25`--- equation (1)

Using differentiation, to differetiate the distance with respect to t.

⇒
`2s (ds)/(dt) = 17000t-90`

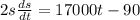
We know, t=0 at the point of intersection of two roads.

∴
`2s (ds)/(dt) = -90`

cross multiplying

`(ds)/(dt) = (-45)/(s)`

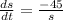
Now, subitituting the value of s in the equation.

∴
`(ds)/(dt) = (-45)/(0.5)`

`(ds)/(dt) = -90`

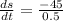
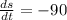
Hence, at 90km/h rate is the distance between the cars decreasing when Joe's car is 0.4 km and Dave's is 0.3 km from the intersection.