Answer:
1) First mistake: 29 - 5 = 24, not -24
Second mistake: Division by negative number changes the sign of inequality. Sam didn't change the sign.
2) 2.5 kg
3) a) no solutions
b) one solution
c) infinitely many solutions
Explanation:
1)Sam solved the following problem:
![-4x+5>29\\ \\-4x+5-5>29-5\ [\text{Sam used the addition property}]\\ \\-4x>24\ [\text{Here Sam made a mistake, because }29-5=24\text{ not }-24]\\ \\(-4x)/(-4)<(24)/(-4)\ [\text{Here Sam made the second mistake}]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/u4bbl3eyv3wwdym3q491wvno6q92mrrkpq.png)
Dividing by negative number changes the sign of the inequality.
Thus,
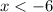
2) Hillary buys 3 pounds of Gala apples which cost $4.50 per pound and paid
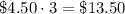
Let x be the number of pounds of Granny Smith apples Hillary bought. She paid $4.50x for x pounds of Granny Smith apples.
The total cost of Hillary buying is $24.75, so
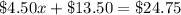
Solve this equation
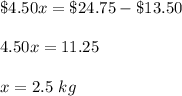
of Granny Smith apples.
3) Consider all equations:
a)
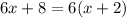
Use distributive property:
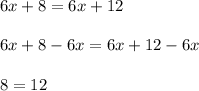
You get false equality, so this equation has no solutions.
b)

Add -5x:
![10x-5x=15+5x-5x\\ \\5x=15\\ \\x=3\ [\text{Divide by 5}]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/8na8yskbrui9uke2luxp9c3dqhizja0jrz.png)
This equation has one solution
c)
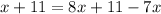
This equation is equivalent to

You get the equality that is true for all values of x, so the equation has infinitely many solutions.