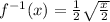Answer:
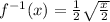
Explanation:
Given:
The function is given as;
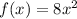
In order to find the inverse, the steps to be followed are:
Step 1: Replace
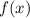 by
by
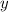 . This gives,
. This gives,
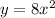
Step 2: Switch 'y' by 'x' and 'x' by 'y'. This gives,
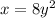
Step 3: Solve for 'y'.
Dividing both sides by 8, we get:
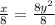
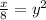 or
or
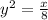
Taking square root on both sides, we get:
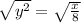
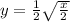
Now, we replace 'y' by
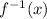 .
.
Therefore, the inverse of the given function is: