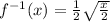Question

F(x)8x^2 find its inverse

Answer 1

`f^(-1)(x)=(1)/(2)\sqrt{(x)/(2)}`

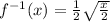
Explanation:

Given:

The function is given as;

`f(x)=8x^2`

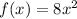
In order to find the inverse, the steps to be followed are:

Step 1: Replace
`f(x)` by
`y`. This gives,

`y=8x^2`

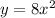
Step 2: Switch 'y' by 'x' and 'x' by 'y'. This gives,

`x=8y^2`

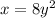
Step 3: Solve for 'y'.

Dividing both sides by 8, we get:

`(x)/(8)=(8y^2)/(8)`

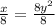
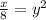`(x)/(8)=y^2` or

`y^2=(x)/(8)`

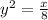
Taking square root on both sides, we get:

`√(y^2)=\sqrt{(x)/(8)}`

`y=(1)/(2)\sqrt{(x)/(2)}`

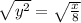
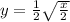
Now, we replace 'y' by
`f^(-1)(x)`.

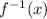Therefore, the inverse of the given function is:

`f^(-1)(x)=(1)/(2)\sqrt{(x)/(2)}`