Question

Use the Ratio Test to determine if the series converges. [infinity]Σ 5k^2/4^kk=1Select the correct choice below and fill in the answer box to complete your choice. A. The series diverges because r=_______B. The series converges because r=_____. C. The Ratio Test is inconclusive because r=_______

Answer 1

B.The series converges because r=1/4

Explanation:

We are given that

`\sum_(k=1)^(\infty)(5k^2)/(4^k)`

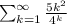
We have to find the correct option.

Ratio test :
`\lim_(k\rightarrow\infty) \mid (a_(k+1))/(a_k)\mid =r`

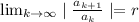
If r< 1 then series convergent

If r>1 then the series divergent

If r=1 , test fails

`r=lim_(k\rightarrow \infty)\mid((5(k+1)^2)/(4^(k+1)))/((5k^2)/(4^k))}\mid`

`r=\lim_(k\rightarrow \infty)\mid{(5(k+1)^2)/(4^k\cdot 4)*(4^k)/(5k^2)}\mid`

`r=\lim_(k\rightarrow \infty)\mid{((k+1)^2)/(4(k^2))\mid`

`r=\lim_(k\rightarrow \infty)\mid(k^2(1+(1)/(k))^2)/(4k^2)\mid`

`r=(1)/(4)`

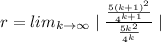
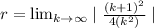
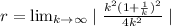
r<1

Therefore, the series converges .

B.The series converges because r=1/4