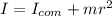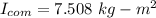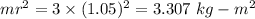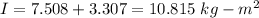Question

An irregular shaped object of mass 3.00 kg has a moment of inertia 7.508 kgm^2 about an axis through a point 1.05 m from its center of mass.Calculate the moment of inertia about a parallel axis through its center of mass.

Answer 1

Answer:
`10.815 kg-m^2`

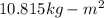
Step-by-step explanation:

Given

mass of object
`m=3 kg`

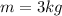
Moment of Inertia of Irregular about an axis passing through an axis
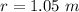`r=1.05\ m` from its center of mass

From parallel axis theorem, the moment of inertia about an axis parallel to an axis passing through the center of mass is equal to the sum of moment of inertia about the center of mass and product of mass and square of the distance of required axis from the center of the mass axis.

`I=I_(com)+mr^2`

`I_(com)=7.508\ kg-m^2`

`mr^2=3* (1.05)^2=3.307\ kg-m^2`

`I=7.508+3.307=10.815\ kg-m^2`