Answer:
Explanation:
Lots of factoring here. Let's rewrite everything in its simplest, factored form:
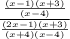
The term (x - 4) cancels out completely, leaving us with
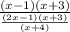
Let's get rid of that (x + 4) by multiplying both top and bottom by (x + 4) to get
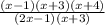
It's obvious now that the (x + 3) term cancels out, leaving us with
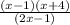
Now all that's left to do is to FOIL out the numerator:
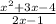
The first choice is the one you want