Question

If m, r, x and y are positive, the ratio of m to r equal to the ratio x to y?(1) The ratio of m to y is equal to the ratio of x to r(2) The ratio of m + x to r + y is equal to the ratio of x to y

Answer 1

Statement (2) is sufficient.

Explanation:

Here, m, r, x and y are positive numbers,

We have to check :

`(m)/(r)=(x)/(y)`

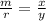
Statement (1) :

The ratio of m to y is equal to the ratio of x to r,

i.e.

`(m)/(y)=(x)/(r)`

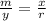
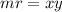`mr = xy` ( By cross multiplication )

Thus, statement (1) is not sufficient.

Statement (2) :

The ratio of m + x to r + y is equal to the ratio of x to y

`(m+x)/(r+y)=(x)/(y)`

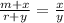
By cross multiplication,

y(m+x) = x(r+y)

By distributive property,

ym + yx = xr + xy

Using subtracting property of equality,

ym = xr

`(m)/(r)=(x)/(y)`

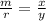
Hence, proved...

i.e. statement (2) is sufficient.