Question

A piece of molding 153 cm long is to be cut to form a rectangular picture frame. What dimensions will enclose the largest area?

Answer 1

Length and width of 38.25 cm each will enclose the largest area.

Explanation:

Let w represent width of rectangle and l represent length of the frame.

We have been given that a piece of molding 153 cm long is to be cut to form a rectangular picture frame. We are asked to find the dimensions of frame that will enclose the largest area.

We can represent our given information in two equation as:

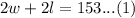`2w+2l=153...(1)` This is our constraint equation.

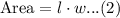`\text{Area}=l\cdot w...(2)` This is our objective equation.

Since our objective is to maximize the area, so we will convert area equation in terms of one variable as:

`2(w+l)=153`

`(2(w+l))/(2)=(153)/(2)`

`w+l=76.5`

`w-w+l=76.5-w`

`l=76.5-w`

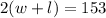
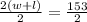
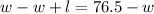
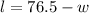
Upon substituting this value in area equation, we will get:

`A=(76.5-w) w`

`A=76.5w-w^2`

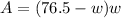
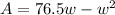
Now, we will find the 1st derivative of area equation as:

`A'=76.5-2w`

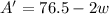
Let us set our derivative equal to 0 to solve for w.

`76.5-2w=0`

`76.5-2w+2w=0+2w`

`76.5=2w`

`(76.5)/(2)=(2w)/(2)`

`38.25=w`

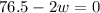
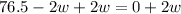
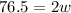
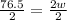
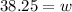
Upon substituting
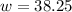`w=38.25` in
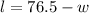`l=76.5-w`, we will get:

`l=76.5-38.25`

`l=38.25`

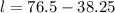
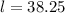
Therefore, the length and width of the frame would be 38.25 cm each and these dimensions will enclose the largest area.