We can rewrite the sphere's equation in Cartesian coordinates.
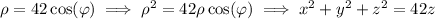
Complete the square to get
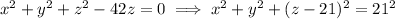
which represents a sphere centered at (0, 0, 21) with radius 21. You can find the sphere's volume easily from here.
But that's not what you're asked to do. You want to find the volume of the intersection of the two spheres. (see attached plot)
The two spheres meet in the plane z = 21/2:

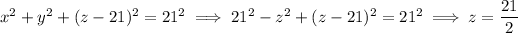
and we express this plane in spherical coordinates as
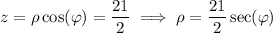
We use this plane to cut the region of interest in half; we have to do this to find the volume because the ρ coordinate does not vary uniformly between the two spheres. On the plus side, the region is symmetrical across this plane, so we only need one integral.
Find the angle φ at which the two spheres meet:
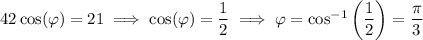
Putting everything together, the volume of the region is
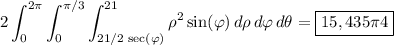
I leave the details of computation to you.