Question

Determine if the lines r1(t) = <3, 0, 2> + t <1, 2, −2> and r2(s) = <0, 1, −1> + s <4, 1, 1> intersect, and if they do, find the point of intersection.

Answer 1

Yes lines are intersecting, point of intersection is <4,2,0>.

Explanation:

Given parametric equations of line are:

`r_(1)(t) = <3, 0, 2> + t <1, 2,-2> \\ r_(1)(t) = <3+t, 0+2t, 2-2t>\\ r_(1)(t) = <3+t, 2t, 2-2t>---(1)`

`r_(2)(s) = <0, 1,-1> + s <4, 1, 1>\\ r_(2)(s) = <0+4s, 1+s,-1+s>\\ r_(2)(s) = <4s, 1+s,-1+s>---(2)\\`

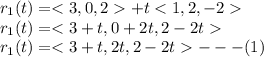
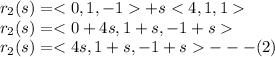
If lines are intersecting then parametric coordinates of (1) are equal to (2)

`3+t=4s---(A)\\2t=1+s---(B)\\2-2t=s-1---(C)\\`

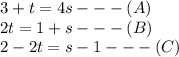
Considering A and B to find values of t and s

From A

t=4s-3---(D)

Putting in (B)

2(4s-3)=1+s

8s-6=1+s

7s=7

s=1

Then

t=4-3

t=1

If lines are intersecting then these values of s and t must satisfy (C)

2-2(1)=1-1

0=0

This shows lines are intersecting.

At this value of t, (1) becomes

`r_(1)(1) = <3+1, 2, 2-2>\\=<4,2,0>`

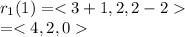
Putting s=1 in (2)

`r_(2)(1)=4, 1+1,-1+1>\\=<4,2,0>`

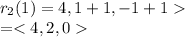
Point of intersection is <4,2,0>.