Question

Marty is proving that the following trigonometric identity is true: tan2θ⋅cos2θ=1−cos2θ Which step would be the first line of his proof?

Answer 1

Explanation:

hope it helps!!

Answer 2

`\text{tan}^2(\theta)\cdot \text{cos}^2(\theta)=\text{sin}^2(\theta)`

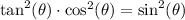
Explanation:

We have been given a trigonometric identity
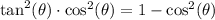`\text{tan}^2(\theta)\cdot \text{cos}^2(\theta)=1-\text{cos}^2(\theta)`. We are asked to determine the first step of the proof.

We will use identity
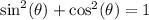`\text{sin}^2(\theta)+\text{cos}^2(\theta)=1` to prove our given identity.

From above identity, we will get:

`\text{sin}^2(\theta)+\text{cos}^2(\theta)-\text{cos}^2(\theta)=1-\text{cos}^2(\theta)`

`\text{sin}^2(\theta)=1-\text{cos}^2(\theta)`

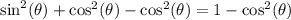
So, we will substitute
`\text{sin}^2(\theta)=1-\text{cos}^2(\theta)` is our given identity as:

`\text{tan}^2(\theta)\cdot \text{cos}^2(\theta)=\text{sin}^2(\theta)`

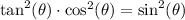
Therefore, the first line of the proof would be
`\text{tan}^2(\theta)\cdot \text{cos}^2(\theta)=\text{sin}^2(\theta)`.

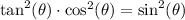Upon dividing both sides of equation by
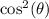`\text{cos}^2(\theta)`, we will get:

`\text{tan}^2(\theta)=\frac{\text{sin}^2(\theta)}{\text{cos}^2(\theta)}`

`\text{tan}^2(\theta)=(\frac{\text{sin}(\theta)}{\text{cos}(\theta)}})^2`

`\text{tan}^2(\theta)=(\text{tan}(\theta)})}^2`

`\text{tan}^2(\theta)=\text{tan}^2(\theta)`

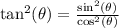
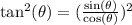
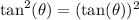
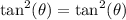
Hence proved.