Question is Incomplete,Complete question is given below;
Figure ABCD is a parallelogram.
What are the lengths of line segments AB and BC?
AB = 4; BC = 16
AB = 4; BC = 8
AB = 10; BC = 20
AB = 10; BC = 28
Answer:
AB = 10 ;BC =28.
Explanation:
The Diagram is missing in the question we have attached the diagram for your reference.
Given:
AB =
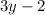
DC =
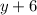
BC =
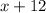
AD =

We need to find the lengths of AB and BC.
Solution:
Since given that Figure ABCD is a parallelogram.
"The opposite side of parallelogram are equal."
Hence we can say that;
AB = DC
Substituting the value we get;

Combining the like terms we get;
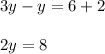
Dividing both side by 2 we get;
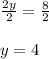
Now AB =

Also
BC = AD
Substituting the value we get;
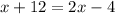
Combining the like terms we get;

Now BC =
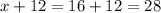
Hence AB = 10 and BC =28.