Answer:
True
Explanation:
A six sigma level has a lower and upper specification limits between
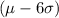 and
and
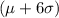 . It means that the probability of finding no defects in a process is, considering 12 significant figures, for values symmetrically covered for standard deviations from the mean of a normal distribution:
. It means that the probability of finding no defects in a process is, considering 12 significant figures, for values symmetrically covered for standard deviations from the mean of a normal distribution:

For those with defects operating at a 6 sigma level, the probability is:
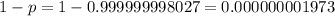
Similarly, for finding no defects in a 5 sigma level, we have:
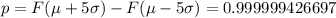 .
.
The probability of defects is:
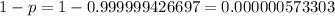
Well, the defects present in a six sigma level and a five sigma level are, respectively:
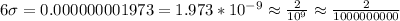
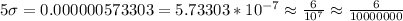
Then, comparing both fractions, we can confirm that a 6 sigma level is markedly different when it comes to the number of defects present:
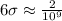 [1]
[1]
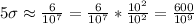 [2]
[2]
Comparing [1] and [2], a six sigma process has 2 defects per billion opportunities, whereas a five sigma process has 600 defects per billion opportunities.