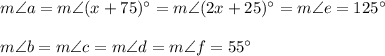Question

PLZ HELP I'M DOING A TEST AND I NEED THIS ANSWER TO PASS IT.

Use the diagarm to the left to answer the following
questions.
PART A. Using parallel line relationships to find the value of x.



PART B. Find the measure of each of the angles. LABEL YOUR ANSWERS.
a = d =
b = e =
c = f =

Answer 1

`x=50\\ \\m\angle a=m\angle (x+75)^(\circ)=m\angle (2x+25)^(\circ)=m\angle e=125^(\circ)\\ \\m\angle b=m\angle c=m\angle d=m\angle f=55^(\circ)`

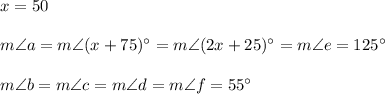
Explanation:

Part A.

Angles with measures
`(2x+25)^(\circ)` and
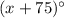`(x+75)^(\circ)` are alternate interior angles when two parallel lines are cut by a transversal. By Alternate Interior Angles theorem,

`2x+25=x+75\\ \\2x-x=75-25\\ \\x=50`

Part B.

Angles a and
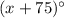`(x+75)^(\circ)` are congruent as vertical angles, so

`m\angle a=(50+75)^(\circ)=125^(\circ)`

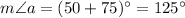
Angles
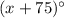`(x+75)^(\circ)` and d are the same side interior angles, so the add up to 180°, thus

`m\angle d=180^(\circ)-125^(\circ)=55^(\circ)`

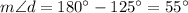
Angles d and f are congruent as vertical angles.

Angles e and
`(2x+25)^(\circ)` are congruent as vertical angles.

Angles c and d are congruent as alternate interior angles.

Angles c and b are congruent as vertical angles.

Therefore,

`m\angle a=m\angle (x+75)^(\circ)=m\angle (2x+25)^(\circ)=m\angle e=125^(\circ)\\ \\m\angle b=m\angle c=m\angle d=m\angle f=55^(\circ)`