Answer:

Explanation:
The correct question is
Which equation represents a parabola that opens upward, has a minimum value of y=3, and has an axis of symmetry at x= 3?
Verify each case
case 1) we have
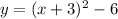
This a vertical parabola open upward (the leading coefficient is positive)---> is ok
The vertex represent a minimum ---> is ok
The vertex is the point (-3,-6)
The minimum value of y=-6 ----> is not ok
The axis of symmetry is x=-3 ----> is not ok
case 2) we have
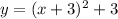
This a vertical parabola open upward (the leading coefficient is positive)---> is ok
The vertex represent a minimum ---> is ok
The vertex is the point (-3,3)
The minimum value of y=3 ----> is ok
The axis of symmetry is x=-3 ----> is not ok
case 3) we have
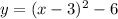
This a vertical parabola open upward (the leading coefficient is positive)---> is ok
The vertex represent a minimum ---> is ok
The vertex is the point (3,-6)
The minimum value of y=-6 ----> is not ok
The axis of symmetry is x=3 ----> is ok
case 4) we have

This a vertical parabola open upward (the leading coefficient is positive)---> is ok
The vertex represent a minimum ---> is ok
The vertex is the point (3,3)
The minimum value of y=3 ----> is ok
The axis of symmetry is x=3 ----> is ok