Question

PLEASE HELP ME IM STRUGGLING!!!

Answer 1

The required answer is
`c=7√(3)`

Therefore the number in green box should be 7.

Explanation:

Given:

AB = 7√2

AD = a , BD = b , DC = c , AC = d

∠B = 45°, ∠C = 30°

To Find:

c = ?

Solution:

In Right Angle Triangle ABD Sine identity we have

`\sin B = \frac{\textrm{side opposite to angle B}}{Hypotenuse}\\`

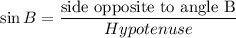
Substituting the values we get

`\sin 45 = (AD)/(AB)= (a)/(7√(2))`

`(1)/(√(2))= (a)/(7√(2))\\\\\therefore a=7`

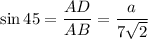
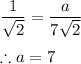
Now in Triangle ADC Tangent identity we have

`\tan C = \frac{\textrm{side opposite to angle C}}{\textrm{side adjacent to angle C}}`

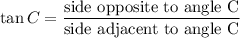
Substituting the values we get

`\tan 30 = (AD)/(DC)= (a)/(c)\\\\(1)/(√(3))=(7)/(c)\\\\\therefore c=7√(3)`

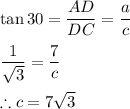
The required answer is
`c=7√(3)`