Question

. Find the area of the regular dodecagon inscribed in a circle if one vertex is at (3, 0).

Answer 1

Area of the regular dodecagon inscribed in a circle will be 27 square units.

Explanation:

A regular dodecagon is the structure has twelve sides and 12 isosceles triangles inscribed in a circle as shown in the figure attached.

Since angle formed at the center by a polygon =
`(360)/(n)`

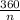
Therefore, angle at the center of a dodecagon =
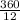`(360)/(12)` = 30°

Since one of it's vertex is (3, 0) therefore, one side of the triangle formed or radius of the circle = 3 units

Now area of a small triangle =
`(1)/(2).(a).(b).sin\theta`

where a and b are the sides of the triangle and θ is the angle between them.

Now area of the small triangle =
`(1)/(2).(3).(3).sin30`

=
`(9)/(4)`

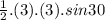
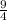
Area of dodecagon = 12×area of the small triangle

= 12×
`(9)/(4)`

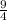
= 27 unit²

Therefore, area of the regular octagon is 27 square unit.