To solve this problem we will apply the concepts related to the calculation of the given speed depending on the height and gravity, as well as the calculation of the kinetic energy and the time elapsed in the occurrence of the phenomena. These processes will be compared between the two objects to conclude the correct answers.
The velocity of the ball one with 1 kg is

The velocity of the ball two with 1 kg is
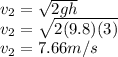
The kinetic energy of ball one is
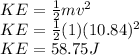
The kinetic energy of the ball two
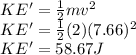
Kinetic energy are almost the same.
Time taken for the fall in free falling for ball one
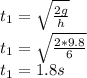
Time taken for the fall in free falling of ball two
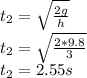
Time taken for both are different
Therefore the correct option are:
D and B.