Question

1. Solve the following equation using the quadratic formula: 3x2 + 6x + 8 = 6.

2. Is the quadratic formula the most efficient way to solve this equation? Why or why not?

Answer 1

1.
`x=-(3+√(3))/(3)\text{ (or) }x=(-3+√(3))/(3)`

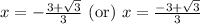
2. Quadratic formula is the most efficient way to solve this equation.

Explanation:

We have been given an equation
`3x^2+6x+8 = 6`. We are asked to solve our given equation using quadratic formula.

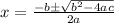`x=(-b\pm√(b^2-4ac))/(2a)`, where,

b = Coefficient of x term,

c = Constant,

a = Coefficient of
`x^2` term.

`3x^2+6x+8-6=6-6`

`3x^2+6x+2=0`

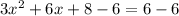
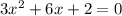
Upon substituting our given values, we will get:

`x=(-6\pm√(6^2-4(3)(2)))/(2(3))`

`x=(-6\pm√(36-24))/(6)`

`x=(-6\pm√(12))/(6)`

`x=(-6\pm √(4\cdot 3))/(6)`

`x=(-6\pm 2√(3))/(6)`

`x=(-6-2√(3))/(6)\text{ (or) }x=(-6+2√(3))/(6)`

`x=(-2(3+√(3)))/(2*3)\text{ (or) }x=(2(-3+√(3)))/(2*3)`

`x=-(3+√(3))/(3)\text{ (or) }x=(-3+√(3))/(3)`

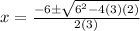
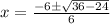
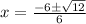
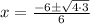
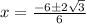
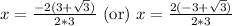
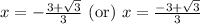
Therefore, the solutions for our given equation are
`x=-(3+√(3))/(3)\text{ (or) }x=(-3+√(3))/(3)`.

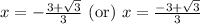2. We cannot factor our given equation by splitting the middle term because there are no such numbers which add up-to 6 and whose product is 6.

Therefore, the quadratic formula is the most efficient way to solve this equation.