Question

Ethanol melts at -114 degree C. The enthalpy of fusion

is5.02KJ/mol. The specific heat of solid and liquid ethanol are
0.97JK/g-K and 2.31 J/g-K, respectively. How much heat(KJ) is
needed toconvert 25.0 g of solid ethanol at -135 degree C to liquid
ethanolat -50 degree C?

Answer 1

Answer: The heat required is 6.88 kJ.

Step-by-step explanation:

The conversions involved in this process are :

`(1):ethanol(s)(-135^0C)\rightarrow ethanol(s)(-114^0C)\\\\(2):ethanol(s)(-114^0C)\rightarrow ethanol(l)(-114^0C)\\\\(3):ethanol(l)(-114^0C)\rightarrow ethanol(l)(-50^0C)`

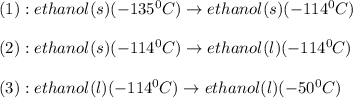
Now we have to calculate the enthalpy change.

`\Delta H=[m* c_(p,s)* (T_(final)-T_(initial))]+n* \Delta H_(fusion)+[m* c_(p,l)* (T_(final)-T_(initial))]+n* \Delta H_(vap)+[m* c_(p,g)* (T_(final)-T_(initial))]`

where,

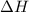`\Delta H` = enthalpy change = ?

m = mass of ethanol = 25.0 g

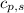`c_(p,s)` = specific heat of solid ethanol= 0.97 J/gK

`c_(p,l)` = specific heat of liquid ethanol = 2.31 J/gK

n = number of moles of ethanol =
`\frac{\text{Mass of ethanol}}{\text{Molar mass of ethanol}}=(25.0g)/(46g/mole)=0.543mole`

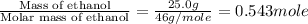
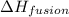`\Delta H_(fusion)` = enthalpy change for fusion = 5.02 KJ/mole = 5020 J/mole

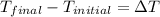`T_(final)-T_(initial)=\Delta T` = change in temperature

The value of change in temperature always same in Kelvin and degree Celsius.

Now put all the given values in the above expression, we get

`\Delta H=[25.0 g* 0.97J/gK* (-114-(-135)K]+0.534mole* 5020J/mole+[25.0g* 2.31J/gK* (-50-(-114))K]`

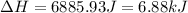`\Delta H=6885.93J=6.88kJ` (1 KJ = 1000 J)

Therefore, the heat required is 6.88 kJ