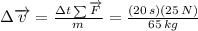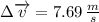Answer:
The skier's change in velocity is 7.69 meters per second.
Step-by-step explanation:
The Newton's second law tells force is equal to the change on the linear momentum of a body:
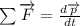
If we approximate the differential
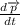 to
to
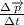 :
:
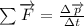
Using that linear momentum is mass times velocity:
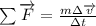
Solving for
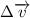 :
: