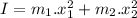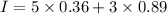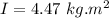Question

A light meterstick is loaded with masses of5.0 kg and 3.0 kg

at the 36 cm and89 cm positions, respectively. What is the moment
of inertiaabout an axis through the 0 cm end of the
meterstick?

Answer 1

`I=4.47\ kg.m^(2)`

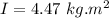
Step-by-step explanation:

Given:

A light meter stick (assuming mass-less) is loaded with point masses at the following positions.

• mass of first object,
  `m_1=5\ kg`

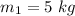
• mass of second object,
  `m_2=3\ kg`

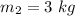
• position of the first mass,
  `x_1=36\ cm=0.36\ m`

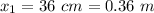
• position of the second mass,
  `x_2=89\ cm=0.89\ m`

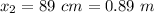
As we know that moment of inertia for point mass is given by:

`I=m.R^2`

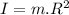
where:

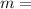`m=` mass of the object

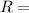`R=` radial distance from the axis of rotation

Now the total moment of inertia:

`I=m_1.x_1^2+m_2.x_2^2`

`I=5* 0.36+3* 0.89`

`I=4.47\ kg.m^(2)`

Answer 2

Answer:
`I=3.024\ kg-m^2`

Step-by-step explanation:

Given

mass of first
`m_1=5 kg`

mass of second
`m_2=3 kg`

Distance of
`m_1` from origin
`r_1=36 cm`

Distance of
`m_2` from origin
`r_2=89 cm`

Moment of inertia is given by multiplication of mass and square of distance

`I=\sum mr^2`

`I=m_1r_1^2+m_2r_2^2`

`I=5* 0.36^2+3* 0.89^2`

`I=0.648+2.376`

`I=3.024\ kg-m^2`