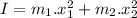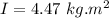Answer:
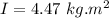
Step-by-step explanation:
Given:
A light meter stick (assuming mass-less) is loaded with point masses at the following positions.
- mass of first object,
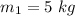
- mass of second object,
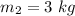
- position of the first mass,
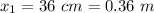
- position of the second mass,
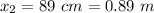
As we know that moment of inertia for point mass is given by:
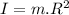
where:
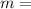 mass of the object
mass of the object
 radial distance from the axis of rotation
radial distance from the axis of rotation
Now the total moment of inertia: