Question

A house has well insulated walls. It contains a volume of

100m^3 of air at 300 K. Calculate the energy required to incrrease
thetemperature of the diatomic ideal gas by 1 degree C.

Answer 1

The energy required to increase the temperature of the diatomic ideal gas by 1 degree C is 118.18 kJ.

Step-by-step explanation:

Given that,

Volume = 100 m³

Temperature = 300 K

Suppose Consider heating it at constant pressure.

We need to calculate the energy required to increase the temperature of the diatomic ideal gas by 1 degree C

Using formula of heat energy

`Q=nC_(p)\Delta T`

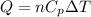
Where, n = numbers of moles of gas

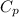`C_(p)` =specific heat capacity

`\Delta T` = change in temperature

We know that,

The specific heat capacity for diatomic ideal gas

`C_(p)=(7R)/(2)`

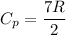
Put the value into the formula of heat

`Q=(7)/(2)nR\Delta T`

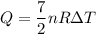
Substitute the value of nR into the formula

`Q=(7)/(2)(PV)/(T)\tiiems\Delta T`

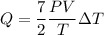
Here, P = pressure of the air

V = volume of the air

Put the value into the formula

`Q=(7)/(2)*(1.013*10^5*100)/(300)*1`

`Q=118183.3\ J`

`Q=118.18\ kJ`

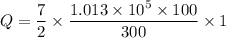
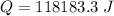
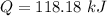
Hence, The energy required to increase the temperature of the diatomic ideal gas by 1 degree C is 118.18 kJ.