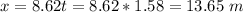Question

A man is shot out of a canon at an angle of 42.0 degrees

abovethe horizontal with an initial speed of 11.60 m/s. Determine
thelocation for the safety net.

Answer 1

To determine the location of the safety net, we need to find the horizontal distance traveled by the man when he lands. First, we find the horizontal component of the initial velocity. Next, we calculate the time of flight using the vertical component of the initial velocity. Finally, we find the horizontal distance using the equation d = v_x * t.

Step-by-step explanation:

To determine the location of the safety net, we need to find the horizontal distance traveled by the man when he lands. We can break the initial velocity into horizontal and vertical components using trigonometry. The horizontal component of the initial velocity can be found using the equation v_x = v * cos(theta), where v is the initial velocity and theta is the launch angle. In this case, v = 11.60 m/s and theta = 42.0 degrees. Therefore, v_x = 11.60 * cos(42.0) = 8.25 m/s. Next, we can determine the time of flight using the vertical component of the initial velocity. The equation for the time of flight is t = 2 * v_y / g, where v_y is the vertical component of the initial velocity and g is the acceleration due to gravity. In this case, v_y = v * sin(theta) = 11.60 * sin(42.0) = 7.70 m/s and g = 9.8 m/s^2. Therefore, t = 2 * 7.70 / 9.8 = 1.57 seconds.

Finally, we can find the horizontal distance traveled by the man using the equation d = v_x * t, where d is the horizontal distance and t is the time of flight. Plugging in the values, d = 8.25 * 1.57 = 12.95 meters. Therefore, the location for the safety net should be approximately 12.95 meters away from the cannon.

Answer 2

The safety net should be 13.65 m away from the canon.

Step-by-step explanation:

The location for the safety net should be exactly at the position where the man will hit the ground.

This is a projectile motion.

We should separate the motion into x- and y-components, and investigate separately.

`v_0 = 11.6~m/s\\v_0_x = v_0\cos(42^\circ) = 8.62~m/s\\v_0_y = v_0\sin(42^\circ) = 7.76~m/s`

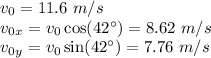
On the x-direction, there is no acceleration, so the kinematics relations are

`x = v_0_x t = 8.62t`

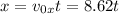
On the y-direction, there is gravitational acceleration, -9.8. We will look for the time that takes for the man to hit the ground. The kinematics relations are

`y - y_0 = v_0_yt -(1)/(2)at^2\\0 - 0 = 7.76t - (1)/(2)9.8t^2\\0 = 7.76t - 4.9t^2\\t = 0 ~and ~ t = 1.58s`

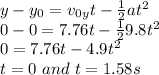
Of course, we will not choose t = 0, since we know that t = 0 is the initial time.

We will plug this into the x-direction equation.

`x = 8.62t = 8.62*1.58 = 13.65~m`