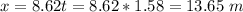Answer:
The safety net should be 13.65 m away from the canon.
Step-by-step explanation:
The location for the safety net should be exactly at the position where the man will hit the ground.
This is a projectile motion.
We should separate the motion into x- and y-components, and investigate separately.

On the x-direction, there is no acceleration, so the kinematics relations are
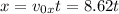
On the y-direction, there is gravitational acceleration, -9.8. We will look for the time that takes for the man to hit the ground. The kinematics relations are
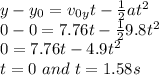
Of course, we will not choose t = 0, since we know that t = 0 is the initial time.
We will plug this into the x-direction equation.