Question

A 1.58-kg steel sphere will not fit through a circular hole in

a0.752-kg aluminum plate, becuase the radius of the sphere is
0.10%larger than the radius of the hole. If both the sphere and
theplate are kept at the same temperature, how much heat must be
putinto the two so that the ball just passes through the hole?

Answer 1

Therefore it is not possible because aluminium will melt first at 939.82 kelvin.

Step-by-step explanation:

Given:

• mass of steel sphere,
  `m_s=1.58\ kg`

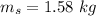
• mass of aluminium plate,
  `m_a=0.752\ kg`

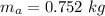
radius of sphere is 10% larger than the radius of the hole in aluminium plate.

We have:

• density of steel,
  `\rho_s=7750\ kg.m^(-3)`

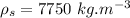
• coefficient of linear thermal expansion of aluminium,
  `\alpha_a=23* 10^(-6)\ m.m^(-1).^(\circ)C^(-1)`

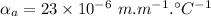
• coefficient of volumetric thermal expansion of steel,
  `\alpha_s=17* 10^(-6)\ m^3.m^(-3).^(\circ)C^(-1)`

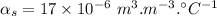
Now, we find the volume of the given sphere:

`V=(m)/(\rho_s)`

`V=(1.58)/(7750)`

`V=2.0387* 10^(-4)\ m^3`

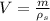
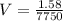
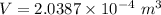
We know that the volume of sphere is given as:

`V=(4)/(3)\pi.r^3`

`r=0.0365\ m`

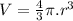
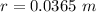
Now the perimeter of the of the 2-D projection of the sphere:

`P=2\pi.r`

`P=2\pi* 0.0365`

`P=0.2293\ m`

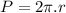
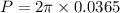
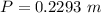
Therefore radius of hole in the aluminium plate:

`r=1.10* r_h`

`r_h=(r)/(1.10)`

`r_h=(0.0365)/(1.10)`

`r_h=0.0332\ m`

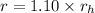
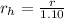
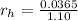
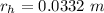
Now experiment of the hole:

`P_h=2\pi.r_h`

`P_h=2\pi* 0.0332`

`P_h=0.2085\ m`

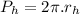
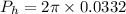
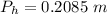
We know the equation of linear thermal expansion is given as:

`\delta l=l.\alpha.\Delta T`

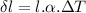
where:

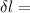`\delta l=` change in length due to change in temperature

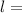`l=` initial original length

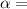`\alpha =`coefficient of linear thermal expansion

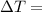`\Delta T=` change in temperature

Now, using the above concept:

`P+\delta P=P_h+\delta P_h`

`0.2293+P* \alpha_s* \Delta T=0.2085+P_h* \alpha_a* \Delta T`

`0.2293+0.2293* (17* 10^(-6))* \Delta T=0.2085+0.2085* \(23* 10^(-6))* \Delta T`

`0.8974* 10^(-6)* \Delta T=0.0208`

`\Delta T=23178.06\ K`

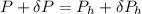
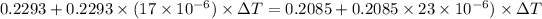
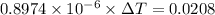
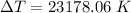
Therefore it is not possible because aluminium will melt first at 939.82 kelvin.