Answer:
Therefore it is not possible because aluminium will melt first at 939.82 kelvin.
Step-by-step explanation:
Given:
- mass of steel sphere,
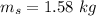
- mass of aluminium plate,
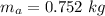
radius of sphere is 10% larger than the radius of the hole in aluminium plate.
We have:
- density of steel,

- coefficient of linear thermal expansion of aluminium,
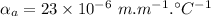
- coefficient of volumetric thermal expansion of steel,
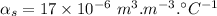
Now, we find the volume of the given sphere:
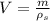
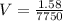
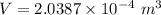
We know that the volume of sphere is given as:
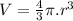
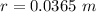
Now the perimeter of the of the 2-D projection of the sphere:
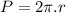
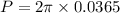
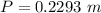
Therefore radius of hole in the aluminium plate:
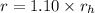
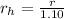


Now experiment of the hole:
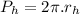
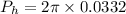

We know the equation of linear thermal expansion is given as:
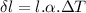
where:
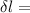 change in length due to change in temperature
change in length due to change in temperature
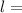 initial original length
initial original length
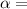 coefficient of linear thermal expansion
coefficient of linear thermal expansion
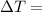 change in temperature
change in temperature
Now, using the above concept:
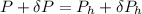

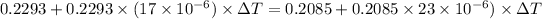
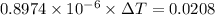
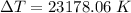
Therefore it is not possible because aluminium will melt first at 939.82 kelvin.