Question

The drawing shows a tire of radius R on a moving car

andidentifies a point P that is at a distance H above theground.
The velocity of this point with respect to the groundhas the same
magnitude v as the linear velocity of the car. Find the ratio
H/R.

Answer 1

H / R = 2/3

Step-by-step explanation:

Let's work this problem with the concepts of energy conservation. Let's start with point P, which we work as a particle.

Initial. Lowest point

Em₀ = K = 1/2 m v²

Final. In the sought height

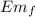`Em_(f)` = U = mg h

Energy is conserved

Em₀ =
`Em_(f)`

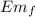
½ m v² = m g h

v² = 2 gh

Now let's work with the tire that is a cylinder with the axis of rotation in its center of mass

Initial. Lower

Em₀ = K = ½ I w²

Final. Heights sought

Emf = U = m g R

Em₀ =
`Em_(f)`

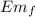
½ I w² = m g R

The moment of inertial of a cylinder is

I =
`I_(cm)` + ½ m R²

I= ½
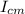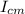`I_(cm)` + ½ m R²

Linear and rotational speed are related

v = w / R

w = v / R

We replace

½
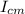`I_(cm)` w² + ½ m R² w² = m g R

moment of inertia of the center of mass

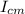`I_(cm)` = ½ m R²

½ ½ m R² (v²/R²) + ½ m v² = m gR

m v² ( ¼ + ½ ) = m g R

v² = 4/3 g R

As they indicate that the linear velocity of the two points is equal, we equate the two equations

2 g H = 4/3 g R

H / R = 2/3