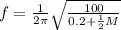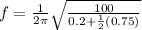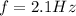To solve this problem we will apply the equations related to the description of Force and Torque in the three given objects. Both in the spring, as in the hanging mass and the pulley. From there we will obtain the relation given for the Amplitude and therefore the direct calculation of the frequency. We can write the following equations of motion:
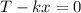 (describes the spring)
(describes the spring)
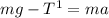
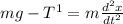 (for the hanging object)
(for the hanging object)
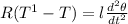
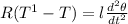 (for the pulley)
(for the pulley)
With the moment of intertia equal to
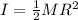
We can combine these equations gives the equation of motion
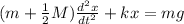
The solution is
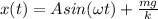
Where
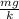 arises because of the extension of the spring due to the weight of the hanging object
arises because of the extension of the spring due to the weight of the hanging object
With the frequency:
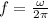
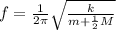
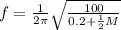
A) For M = 0kg
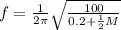
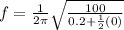
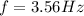
B) For M = 0.250kg
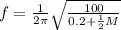
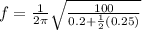
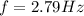
C) For M = 0.750kg