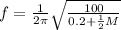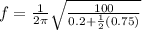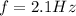Question

One end of a light spring with force constant 100 N/m

isattached to a vertical wall. A light string is tied to the
otherend of of the horizontal spring. The string changes from
horizontalto vertical as it passes over a solid pulley of diameter
4.00 cm.The pulley is free to turn on a fixed smooth axle. The
verticalsection of the string supports a 200 g object. The string
does notslip at its contact with the pulley. Find the frequency
ofoscillation of the object if the mass of the pulley is
a)negligible, b) 250 grams, and c) 750g.

Answer 1

Please see updated attachment

Step-by-step explanation:

Please see updated attachment

Answer 2

To solve this problem we will apply the equations related to the description of Force and Torque in the three given objects. Both in the spring, as in the hanging mass and the pulley. From there we will obtain the relation given for the Amplitude and therefore the direct calculation of the frequency. We can write the following equations of motion:

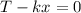`T-kx = 0` (describes the spring)

`mg -T^1 = ma`

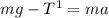
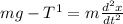`mg -T^1 = m(d^2x)/(dt^2)` (for the hanging object)

`R(T^1-T) = l (d^2\theta)/(dt^2)`

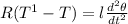
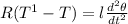`R(T^1-T) = l (d^2\theta)/(dt^2)` (for the pulley)

With the moment of intertia equal to

`I= (1)/(2) MR^2`

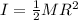
We can combine these equations gives the equation of motion

`(m+(1)/(2)M)(d^2x)/(dt^2)+kx = mg`

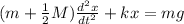
The solution is

`x(t) = Asin(\omega t) +(mg)/(k)`

Where
`(mg)/(k)` arises because of the extension of the spring due to the weight of the hanging object

With the frequency:

`f = (\omega)/(2\pi)`

`f = (1)/(2\pi) \sqrt{(k)/(m+(1)/(2)M)}`

`f = (1)/(2\pi) \sqrt{(100)/(0.2+(1)/(2)M)}`

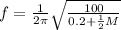
A) For M = 0kg

`f = (1)/(2\pi) \sqrt{(100)/(0.2+(1)/(2)M)}`

`f = (1)/(2\pi) \sqrt{(100)/(0.2+(1)/(2)(0))}`

`f = 3.56Hz`

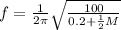
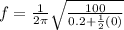
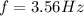
B) For M = 0.250kg

`f = (1)/(2\pi) \sqrt{(100)/(0.2+(1)/(2)M)}`

`f = (1)/(2\pi) \sqrt{(100)/(0.2+(1)/(2)(0.25))}`

`f = 2.79Hz`

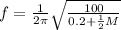
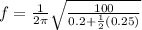
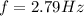
C) For M = 0.750kg

`f = (1)/(2\pi) \sqrt{(100)/(0.2+(1)/(2)M)}`

`f = (1)/(2\pi) \sqrt{(100)/(0.2+(1)/(2)(0.75))}`

`f = 2.1Hz`