Question

4. Could a circle given by the equation (xx−5)2+(yy−1)2=25 have tangent lines given by the equations

y−4=4/3(x−1) and y−5=3/4(x−8)? Explain how you know.

Answer 1

Tangent, not a tangent

Explanation:

Given that a circle has equation as

`(x-5)^2+(y-1)^2=25`

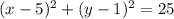
We have to check whether the two lines are tangents to the circle

I line:

`y−4=(4)/(3) (x−1)`

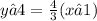
Substitute for y from straight line equation in the circle equation and check whether equal solutions are there. If equal solutions, then the line is tangent.

`(x-5)^2 + ((4x)/(3) +(5)/(3) )^2 =25\\x^2-10x+(16x^2)/(9) +(25)/(9) +(40x)/(9) =0\\25x^2-25x+25=0\\x=1,1`

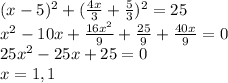
Since equal roots are there this is a tangent

II line.

Substiutte for y to get

`(x-5)^2 +((3x)/(4) -2)^2 =25\\x^2-10x +(9x^2)/(16) +4-3x=0\\25x^2-208x+64 =0\\`

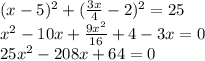
Here discriminant not equals 0

Not equal roots

So cannot be a tangent.