Answer:
Tangent, not a tangent
Explanation:
Given that a circle has equation as
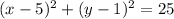
We have to check whether the two lines are tangents to the circle
I line:
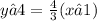
Substitute for y from straight line equation in the circle equation and check whether equal solutions are there. If equal solutions, then the line is tangent.
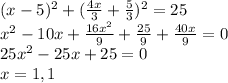
Since equal roots are there this is a tangent
II line.
Substiutte for y to get
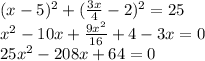
Here discriminant not equals 0
Not equal roots
So cannot be a tangent.