Answer
given,
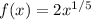
interval = [-32, 32]
differentiating the given equation
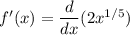

hence, the above solution is not defined at x = 0
and x = 0 lie in the given interval i.e. [-32, 32]
so, at x = 0 the function is not differentiable.
Hence, mean value theorem does not apply to the given function.