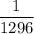Question

What is the probability of rolling four successive 6's
withfour rolls of a fair die?

Answer 1

Answer:
`(1)/(1296)`

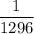
Explanation:

Formula of probability :
`\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

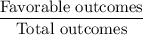
Total number of outcomes for a fair die = 6 (From 1 to 6)

When we roll a die , Favorable outcome of getting six =1

So , The probability of getting a six : P(rolling a six)=
`(1)/(6)`

Since the events of throwing a fair die again and again are independent events.

So , Probability of rolling four successive 6's with four rolls of a fair die

= P(rolling a six) x P(rolling a six) x P(rolling a six) x P(rolling a six) [If event are independent then probability of all occurring together is the product of their individual probability]

=
`(1)/(6)*(1)/(6)*(1)/(6)*(1)/(6)=(1)/(1296)`

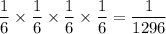
∴ Probability of rolling four successive 6's with four rolls of a fair die=
`(1)/(1296)`