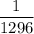Answer:
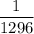
Explanation:
Formula of probability :
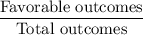
Total number of outcomes for a fair die = 6 (From 1 to 6)
When we roll a die , Favorable outcome of getting six =1
So , The probability of getting a six : P(rolling a six)=

Since the events of throwing a fair die again and again are independent events.
So , Probability of rolling four successive 6's with four rolls of a fair die
= P(rolling a six) x P(rolling a six) x P(rolling a six) x P(rolling a six) [If event are independent then probability of all occurring together is the product of their individual probability]
=
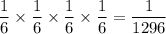
∴ Probability of rolling four successive 6's with four rolls of a fair die=