Question

9. Two points in the plane, A(−3,8) and ????(17,8), represent the endpoints of the diameter of a circle.

a. What is the center of the circle? Explain.
b. What is the radius of the circle? Explain.
c. Write the equation of the circle.

Answer 1

a) (7,8)

b) r = 10

c)
`(x-7)^2+(y-8)^2=100`

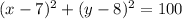
Explanation:

a) Given the endpoints the diameter of the circle as A(-3,8) and B(17,8)

we should realize that the center of the circle lies exactly at the midpoint of these two points. let's denote the midpoint as
`(x_m,y_m)`

`(x_m, y_m) = \left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`(x_m, y_m) = \left((-3+17)/(2),(8+8)/(2)\right)`

`(x_m, y_m) = (7,8)`

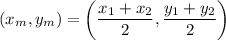
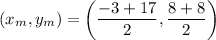
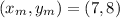
this is the coordinate of the center of the circle.

b) The radius of the circle can be easily found by using the distance formula between the center point and either of the two endpoints of the diameter.

the general distance formula is:

`r = √((x_1-x_2)^2+(y_1-y_2)^2)`

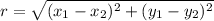
in our case the equation changes to: (selecting the centre and point B)

`r = √((x_m-x_2)^2+(y_m-y_2)^2)`

`r = √((7-17)^2+(8-8)^2)`

`r = 10`

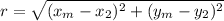
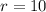
side note: there are more alternate ways to find the radius for e.g (you can use the distance formula between the points A and B and that'll give you the length of the diameter which you can divide by 2 to get the radius) OR (you don't need to use the distance formula at all since in this particular case all the coordinates lie on the same horizontal line, so by simply subtracting the two x-coordinates of the center and either of A or B)

c) the ingredients needed to make the equation of the circle are the

1. coordinates of the center:
   `(x_m,y_m) = (7,8)`
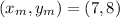
2. radius of the circle:
   `r = 10`

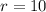
we can put this in the formula of the circle:

`(x-a)^2+(y-b)^2=r^2`

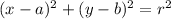
in our case the equation changes to:

`(x-x_m)^2+(y-y_m)^2=r^2`

`(x-7)^2+(y-8)^2=(10)^2`

`(x-7)^2+(y-8)^2=100`

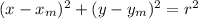
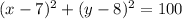
this is the equation of the circle!