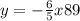Question

A coach is laying out lanes for a race. The lanes are perpendicular to a segment of the track such that one endpoint

of the segment is (2,50), and the other is (20,65). What are the equations of the lines through the endpoints?

Answer 1

`y= -(6)/(5) x +(262)/(5)`

`y= -(6)/(5) x 89`

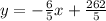
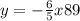
Explanation:

For this case we need to remember that a line is defined with minimum two points. And for this case we have two points given and we want to find a line who fits for the two points.

The two points are (2,50) and (20,65). Let's define some notation:

`x_1 = 2, y_1 = 50 , x_2 = 20, y_2 = 65`

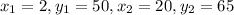
We want to estimate a line
`y = mx+b`

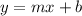
Where m is the slope and b the the intercept. We can find the slope with the following formula:

`m = (\Delta y)/(\Delta x) = (y_2 -y_1)/(x_2 -x_1)= (65-50)/(20-2)=(5)/(6)`

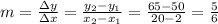
On this case we need "The lanes are perpendicular to a segment of the track", so for this case when we have perpendicular lines we need to satisfy this:

`m_1 *m_2 = -1`

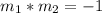
And if we find the slope for the tangent line
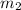`m_2` we got:

`(5)/(6) *m_2 = -1`

`m_2 = -(6)/(5)`

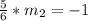
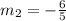
Now with the slope we can find the value of b using the first point, on this case (2,50) and if we replace into our equation we got:

`50 = -(6)/(5) (2) + b`

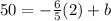
And we can solve for b like this:

`b = 50 + (12)/(5)=(262)/(5)`

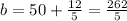
And the first line perpendicular to the point (2,50) would be:

`y= -(6)/(5) x +(262)/(5)`

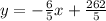
Now with the slope we can find the value of b using the second point, on this case (20,65) and if we replace into our equation we got:

`65 = -(6)/(5) (20) + b`

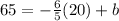
And we can solve for b like this:

`b = 65 + 24=89`

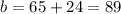
And the first line perpendicular to the point (20,65) would be:

`y= -(6)/(5) x 89`