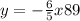Answer:
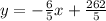
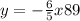
Explanation:
For this case we need to remember that a line is defined with minimum two points. And for this case we have two points given and we want to find a line who fits for the two points.
The two points are (2,50) and (20,65). Let's define some notation:
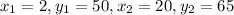
We want to estimate a line
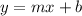
Where m is the slope and b the the intercept. We can find the slope with the following formula:
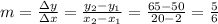
On this case we need "The lanes are perpendicular to a segment of the track", so for this case when we have perpendicular lines we need to satisfy this:
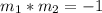
And if we find the slope for the tangent line
 we got:
we got:
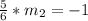

Now with the slope we can find the value of b using the first point, on this case (2,50) and if we replace into our equation we got:
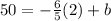
And we can solve for b like this:
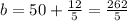
And the first line perpendicular to the point (2,50) would be:
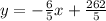
Now with the slope we can find the value of b using the second point, on this case (20,65) and if we replace into our equation we got:
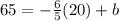
And we can solve for b like this:
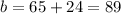
And the first line perpendicular to the point (20,65) would be: