Answer:
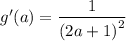
equation of tangent at (1,1/3) is:
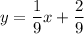
Explanation:
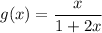
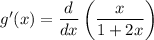
this differentiation can be easily done using the quotient rule:
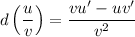
here,
u = x, and v = 1+2x.
u' = 1, and v' = 2
The derivative of u and v are written as u' and v'.

this is the derivative of g(x) and it is denoted by g'(x)
g'(a) means to simply replace all the x's with a in the above equation
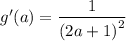
to find the equation of the tangent to this curve at (1,1/3)
we need to know the slope of the tangent at that very point. This can be found using g'(x). since g'(x) only takes x as the input. we'll only use the x-coordinate of the point (1,1/3)
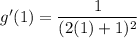
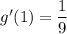
the slope of the tangent to the curve at the point (1,1/3) is 1/9
to find the equation of the line we'll use:
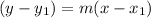
here m is the slope, and (x1,y1) = (1,1/3)

simplify:

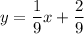
this is the equation of the tangent to the curve g(x) at the point (1,1/3)