Question

If g(x)=x/1+2x, how do you find g'(a) and use it to find an equation of the tangent line to the curve at the point (1, 1/3).

Answer 1

`g'(a)=(1)/(\left(2 a + 1\right)^(2))`

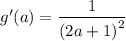
equation of tangent at (1,1/3) is:

`y = (1)/(9)x+(2)/(9)\\`

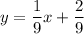
Explanation:

`g(x) = (x)/(1+2x)`

`g'(x) = (d)/(dx)\left((x)/(1+2x)\right)`

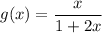
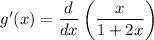
this differentiation can be easily done using the quotient rule:

`d\left((u)/(v)\right) = (vu'-uv')/(v^2)`

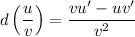
here,

u = x, and v = 1+2x.

u' = 1, and v' = 2

The derivative of u and v are written as u' and v'.

`g'(x)=((1+2x)(1)-(x)(2))/((1+2x)^2)\\g'(x)=(1)/(\left(2 x + 1\right)^(2))`

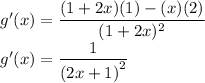
this is the derivative of g(x) and it is denoted by g'(x)

g'(a) means to simply replace all the x's with a in the above equation

`g'(a)=(1)/(\left(2 a + 1\right)^(2))`

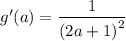
to find the equation of the tangent to this curve at (1,1/3)

we need to know the slope of the tangent at that very point. This can be found using g'(x). since g'(x) only takes x as the input. we'll only use the x-coordinate of the point (1,1/3)

`g'(1)=(1)/((2(1) + 1)^(2))`

`g'(1)=(1)/(9)`

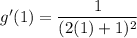
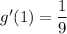
the slope of the tangent to the curve at the point (1,1/3) is 1/9

to find the equation of the line we'll use:

`(y-y_1) = m(x-x_1)\\`

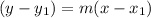
here m is the slope, and (x1,y1) = (1,1/3)

`(y-(1)/(3)) = (1)/(9)(x-1)\\`

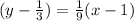
simplify:

`y = (1)/(9)x-\dfra{1}{9}+(1)/(3)\\`

`y = (1)/(9)x+(2)/(9)\\`

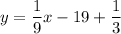
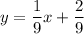
this is the equation of the tangent to the curve g(x) at the point (1,1/3)