Answer:
94°
Explanation:
Oblique triangles are of two types: acute or obtuse triangle. They are not right triangles since they have no right angle.
This question can be answer using the Law of cosines, which states that:
 [1]
[1]
Where
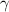 is the angle of the respective opposite side c, a and b are the other triangles' sides.
is the angle of the respective opposite side c, a and b are the other triangles' sides.
Well, since we have all the information needed to find
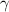 , that is, a = 54, b = 68 and c = 90, we calculate it using the formula [1] as follows:
, that is, a = 54, b = 68 and c = 90, we calculate it using the formula [1] as follows:
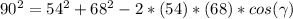
Solving this equation for
 :
:

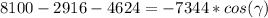
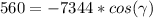
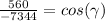
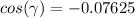 (for four significant figures)
(for four significant figures)
To obtain
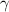 , we need to determine which angle has a
, we need to determine which angle has a
 For this, it is necessary the
For this, it is necessary the
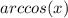 function, also expressed as
function, also expressed as
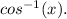
Then
![\\ cos^(-1)[cos(\gamma)] = cos^(-1)(-0.07625)](https://img.qammunity.org/2021/formulas/mathematics/college/stawoii6cya6ugat9wscpmqluqxehr35xn.png)
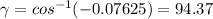 degrees.
degrees.
Rounding the result to the nearest whole number, the answer is
 94°.
94°.
The rest of the angles can be obtained using the Law of sines.