Answer:
The remaining sides are
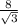 units and
units and
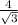 units.
units.
Explanation:
It is given that the interior angles of a right angle triangle are 30, 60, 90 degree. The side opposite of 60 degrees is 4.
In a right angle triangle,

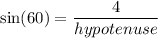
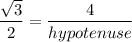

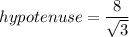
The hypotenuse of the triangle is
 units.
units.
According to the Pythagoras theorem,

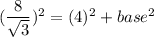
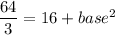
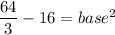
Taking square root on both sides.
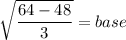
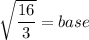
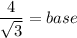
Therefore, the remaining sides are
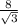 units and
units and
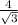 units.
units.